«Cuando se ha eliminado lo imposible, lo que queda, aunque improbable, debe ser la verdad» (Sir Conan Doyle)

En un silencio envolvente se está jugando una partida de ajedrez. Dos humanos fijan su atención en una representación abstracta, imaginando el futuro. Las piezas están repartidas aquí y allá. Configuran una posición. ¿Una posición estática? De ninguna manera. Esta representación encierra un gran dinamismo. De la posición se proyectan múltiples ideas que marcarán el camino de la partida. Pero hay más. En la posición está también la historia de la partida.

El Ajedrez retrospectivo (o retrógrado) mira hacia atrás en el tiempo. Es una forma de análisis que, pese a seguir estrictamente las normas del ajedrez, no tiene nada que ver con el análisis del juego hacia adelante.

En el ajedrez que va hacia adelante, hacia el futuro, el objetivo es encontrar la mejor jugada. A partir de una determinada posición se analizan las posibles jugadas y sus posibles respuestas. Con ello se va creando un árbol de variantes. Dado que en muchos casos es imposible analizar todas las posibilidades, se trabaja en unas jugadas candidatas y se desechan las que en principio se consideran malas. Ahí cuenta mucho la comprensión de la posición, la experiencia y la intuición en la elaboración de planes estratégicos o tácticos. En definitiva, consiste en un proceso de pensamiento creativo que plantea y decide un camino a seguir entre los muchos posibles.

Por el contrario, en el ajedrez que mira hacia atrás, hacia el pasado, el objetivo es desvelar qué ocurrió. Encontrar de qué forma se llegó a una posición determinada, averiguar el único camino posible que nos llevó a la posición. Es un análisis de pura deducción, donde no intervienen ni la estrategia ni la táctica. Lo que hay que averiguar es cómo se llegó aquí.

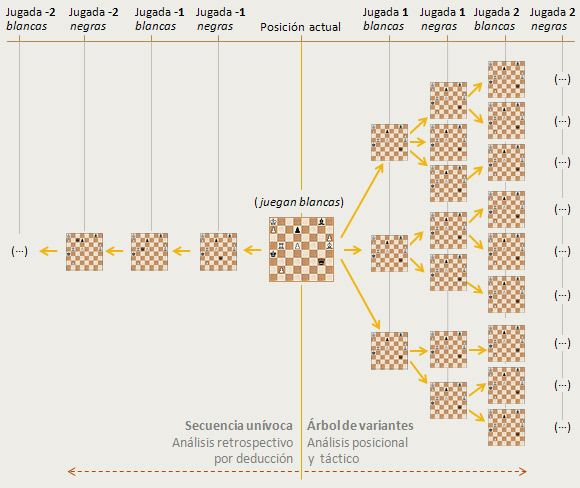
Esta nueva dimensión del juego ha sido abordada por diversos compositores, dando lugar a ingeniosas posiciones que son como el “escenario del crimen”. De la propia posición se puede deducir cuales fueron las posiciones anteriores, qué cosas ocurrieron. Pueden llegar a ser problemas extraordinariamente complejos. He seleccionado algunos ejemplos variados de ajedrez retrospectivo que nos darán una pincelada sobre este vasto y enigmático campo.

Empecemos con un problema muy sencillo:
¿Cual fue la última jugada de las negras?

Antes de seguir leyendo, os invito a perder un par de minutos para deducir qué fue lo que pasó. La lógica de la posición es aplastante.

Razonemos. No hay muchas posibilidades. Las negras movieron su única pieza, el rey. Éste tuvo que venir de a7 pues es imposible que el viniera de b7 o de b8 (el rey blanco está cubriendo estas casillas). Pero la casilla a7 está amenazada por el alfil blanco, o sea, sabemos que el rey recibió un jaque del alfil.

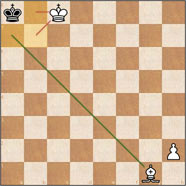
¿Cómo pudo el blanco hacer un jaque con su alfil en la jugada anterior? Este alfil sólo hubiera podido moverse a lo largo de la diagonal g1-a7, pero desde cualquiera de estas casillas ya estaría dando jaque previamente. O sea, el alfil blanco no pudo haber movido.

La única opción posible es que las blancas tuvieran una pieza que obstaculizara la diagonal y, al mover esa pieza, dieron jaque a la descubierta y el rey negro jugó a a8. ¿Dónde está esta pieza? No está. Tuvo que comérsela el rey negro en a8. ¿Qué pieza blanca obstaculizaba el jaque del alfil y fue a b8? Sólo pudo ser un caballo situado en b6. Resulta evidente, pues, que el blanco jugó el caballo de b6 a a8 dando jaque a la descubierta. Y el rey negro capturó el caballo en a8. Sencillo, ¿no?

Veamos ahora un problema retrospectivo compuesto por el escritor ruso americano Vladimir Nabokov, muy conocido por su novela Lolita, y autor de la excelente novela ajedrecística La defensa (ambas llevadas al cine).

Vladimir Nabokov fue un creador de ajedrez poético. Su libro Poems and Problems contiene 53 poemas y 18 problemas de ajedrez. Las composiciones de Nabokov tienen algo especial. Las posiciones que propone son enrevesadas y difícilmente se podrían producir en partidas reales. Sin embargo tienen una belleza y un equilibrio que desbordan la imaginación. Múltiples variantes completamente distintas llevan a un mismo resultado.

En el último problema de Poems and Problems utiliza un bello tema retrospectivo:
Las blancas retiran su última jugada y dan mate.

Aquí se trata de saber cuál fue la última jugada de las blancas, y luego encontrar la jugada alternativa que habría dado el mate. O sea, una jugada hacia atrás y otra jugada hacia adelante.

¿Cuál fue la última jugada de las blancas? No es nada evidente dado que hay muchas jugadas posibles:
– La torre blanca de c7 pudo haber venido de a7, b7, c5, c4, c3, c2 o c1. Y en todos estos casos pudo llegar a la casilla c7 vacía, o bien capturando una pieza negra.
– Podrían haber movido su dama desde g8, h8, f7 o g7
– Podrían haber movido su rey desde f4, f6, g4, g5 o g6

Pero si las blancas rectifican con cualquiera de estos 16 movimientos, no se ve la forma de dar mate en una jugada como pide el enunciado. Las torres y dama negras pueden cubrir todos los posibles jaques (excepto el jaque en c6, que lo controla el peón).

¿Qué otras posibilidades hay? Pues que las blancas hayan llevado un peón a la última fila y hayan promocionado:
– Pudo haber un peón blanco en b7 que capturó en c8 y se convirtió en torre
– Pudo haber un peón blanco en d7 que capturó en c8 y se convirtió en torre
– Pudo haber un peón blanco en f7 que avanzó a f8 y se convirtió en dama
– Pudo haber un peón blanco en g7 que capturó en f8 y se convirtió en dama

De estas cuatro posibilidades sólo hay una que, una vez rectificada, permite a las blancas dar el mate en una jugada:

Había un peón blanco en d7, que capturó un caballo negro en c8 y se convirtió en torre (luego se verá por qué tuvo que haber un caballo en c8).

Ahora las blancas rectifican esta jugada y capturan la torre negra de e8, promocionando a caballo, dando el mate y completando la solución del problema.

Esto explica por qué en c8 había un caballo. No pudo ser una dama o alfil negros puesto que entonces el peón de d7 hubiera estado clavado y no habría podido mover para capturar en e8.

Como apunta el propio Nabokov, «Hay algo suavemente mágico en la transformación retrospectiva de la torre blanca en un caballo negro, y de la torre negra en un caballo blanco, conservando sin embargo la simetría y el dominio de la casilla c7 por parte de las blancas». Apreciémoslo en este diagrama comparativo:

El siguiente ejemplo (de Armand Lapierre, 1959) es muy especial. Se trata de un sencillo problema hacia adelante: Las blancas juegan y dan mate en 2. De entrada parece muy fácil, pero para encontrar la solución correcta debe hacerse un análisis retrospectivo, puesto que entra en escena un elemento de incertidumbre.

La primera jugada 1.Tad1 amenaza 2.Td8 mate, que sólo puede ser defendido por
1…0-0. La cuestión es: “¿Es el enroque negro una jugada legal?”

No se puede probar si las negras pueden o no pueden enrocar. Sin embargo, se puede demostrar que es imposible que las negras y las blancas puedan enrocar al mismo tiempo. Veamos. Consideremos la torre de d4. Si esta es la torre original de a1, evidentemente las blancas no pueden enrocar, puesto que habrían movido las dos torres (ésta y la que ahora está en a1). En el caso de que la torre de d4 fuera la original de h1, entonces el rey blanco tuvo que desplazarse para dejar salir a la torre de la primera fila, por lo que en este caso las blancas tampoco pueden enrocar.

Ahora bien, si se trata de una torre promovida (un peón blanco avanzó hasta la 8ª fila y se convirtió en torre), entonces esta torre blanca tuvo que haber estado en d8, en f8 o en h8. En cualquiera de estas posibilidades, el rey negro (o la torre negra) tuvo que haber movido, por lo que si la torre de e4 fue el resultado de una coronación, las negras no podrían enrocar.

Se puede demostrar, pues, que los dos enroques son mutuamente excluyentes, pero ninguno puede ser demostrado como imposible en sí mismo.

En base a este razonamiento, el intento 1. Tad1?, amenazando 2. Td8 mate, falla ante 1… 0-0! (no hay forma de demostrar que las negras no pueden enrocar), con lo que las negras evitan el mate:

La solución precisa es 1. 0-0-0! y ahora 2.Td8 mate no se puede evitar, puesto que en este caso 1… 0-0 no se podría jugar. Un sencillo problema sutilmente profundo.

Esta posición me causó una honda impresión. A mi modo de ver, nos demuestra con toda claridad la dimensión cuántica del ajedrez. Me explico. “La realidad” a escala atómica tiene unas particularidades asombrosas. Edwing Schrödinger ideó un escenario donde un evento a escala atómica condicionaba la realidad a escala humana.

“El gato de Schrödinger” es un experimento imaginario que expone una de las consecuencias de la mecánica cuántica. El experimento plantea un sistema formado por una caja opaca que contiene un gato encerrado. En la caja también hay una botella de gas venenoso y un dispositivo con una partícula radiactiva, con un 50% de posibilidades de que se desintegre, libere el veneno y el gato muera.

Mientras no se abra la caja, según los principios de la mecánica cuántica, la descripción de este momento (su “función de onda”) es el resultado de la superposición de los estados “vivo” y “muerto”. Existen dos realidades simultáneas. El gato está vivo y el gato está muerto. Sin embargo, una vez se abra la caja, el gato o bien estará vivo o bien estará muerto.

De este sencillo experimento han surgido profundas interpretaciones, por ejemplo la del desdoblamiento en dos universos cada vez que interviene un observador. Tras abrir la caja, el gato está vivo y muerto en dos realidades de dos universos paralelos.

Y ahí reside el fenómeno cuántico observado en esta posición de ajedrez. Mientras las blancas no jueguen, hay diferentes estados de enroque posibles (realidades superpuestas). Es verdad que puede enrocar el blanco (y no el negro) y también es verdad que puede enrocar el negro (y no el blanco).

En el momento en que las blancas juegan, sea cual sea el movimiento realizado, es como abrir la caja del gato: la posibilidad del enroque queda perfectamente determinada.

Los problemas retrospectivos no sólo consisten en hallar los movimientos anteriores de una posición. Por ejemplo, los hay que consisten en determinar de qué color es una pieza, de quién es el turno, cuál es el número mínimo de jugadas para llegar a una determinada posición desde el inicio de una partida, si una posición es legal, o dónde debería estar situada una pieza.

Raymond Smullyan (matemático, lógico, y filósofo) es uno de los mayores expertos en ajedrez retrospectivo, al que ha dedicado dos de sus libros.

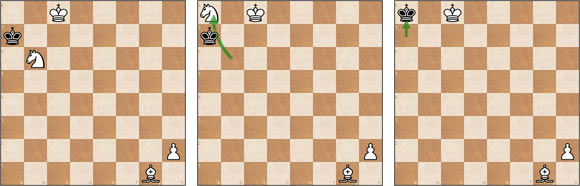
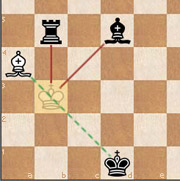
En la introducción de Juegos de ajedrez y los misteriosos caballeros de Arabia nos plantea el siguiente enigma: ¿Dónde está el rey blanco?

Bonita pregunta. De entrada tenemos 60 casillas libres y el rey blanco sólo puede estar en una de ellas. Hay que deducir cuál es esta casilla y demostrar cómo pudo llegar allí.

Razonamiento natural:
Dado que el alfil blanco ahora está amenazando al rey negro, podemos afirmar que:
a) O bien el rey blanco está en b3 cubriendo el jaque.
b) O bien el alfil blanco está dando jaque al rey negro.

El rey blanco no puede estar en b3 puesto que tendría un jaque imposible de dos piezas a la vez: el alfil y la torre negros. Cualquiera de estas piezas no hubiera podido mover para dar jaque, ya que la otra estaría dando jaque previamente.
Por lo tanto, el rey blanco no está en b3 y el rey negro está en jaque.

¿Cómo han dado las blancas el jaque? Con el alfil es imposible pues sólo puede moverse por la diagonal en la que está haciendo el jaque. Así pues, el rey blanco hubiera tenido que mover desde b3 dando jaque a la descubierta. (Evidentemente no podía venir de c2 donde estaría tocando al rey negro).

Pero si venía de b3, no podría estar en el jaque imaginario de torre y alfil a la vez …

En conclusión, la posición es imposible, es una paradoja. Dicho esto, tomaros otro minuto para averiguar qué demonios pasó.

Bien. Pues resulta que el razonamiento expuesto anteriormente no es válido.

Indudablemente el rey blanco no puede estar ahora en b3. Pero eso no significa que no acabe de llegar desde allí. Antes, quizás sí podía estar en b3 y se retiró para dar el jaque a la descubierta.

Imaginemos que el rey blanco acaba de capturar una pieza negra. Pongamos el rey blanco en b3 y un peón negro en c3. Esta sería la posición del último movimiento.

Ahora bien, ¿cómo hicieron las negras jaque al rey blanco? Sólo fue posible moviendo el peón negro que acabamos de poner: Este peón venía de b4 y capturó al paso otro peón blanco que estaba en c4.

Pongamos entonces el peón negro b4 y un peón blanco en c4: Esta fue la posición de la jugada anterior, donde el rey blanco estaba protegido de los jaques de la torre y el alfil por ambos peones, a la vez que cubría el jaque del alfil blanco sobre el rey negro.

Retrocedamos otra jugada: Para que el peón negro hiciera una captura al paso, debemos poner el peón blanco en c2.

Ahora el alfil negro está dando jaque, con lo que se deduce que este alfil acaba de mover.

Retrocedemos otro movimiento y ponemos el alfil negro en cualquier punto de la diagonal h1-a8 para poder dar este jaque, por ejemplo en e4.

Y así, sólo sabiendo lo que pasó, podemos dar respuesta al enigma: El rey blanco está en c3.

Y sólo pudo llegar ahí con la secuencia de jugadas que hemos descubierto:

Veamos ahora un problema retrospectivo que aparece en la novela de Arturo Pérez-Reverté “La tabla de Flandes”, donde la trama sigue el hilo de una partida de ajedrez. A diferencia de Lewis Carroll (ver Alicia en el país del ajedrez), Pérez-Reverté engarza los acontecimientos del relato con una secuencia de movimientos de rigor ajedrecístico.

Situémonos. Una joven está restaurando un cuadro de un pintor flamenco del siglo XV. En la pintura se muestran dos nobles caballeros jugando una partida de ajedrez, y en segundo plano, una dama vestida de negro leyendo un libro.

Tras realizar unas placas radiológicas, aparece una inscripción escondida: Quis necavit equitem (“¿Quién mató al caballero?”). Con ello empieza una investigación en la que tomarán parte la joven restauradora, un anticuario homosexual y un excéntrico jugador de ajedrez.

Me referiré aquí a la primera parte de la novela. A partir de la posición mostrada en la pintura, el ajedrecista investiga la historia de la posición, los movimientos previos que se jugaron cinco siglos atrás en aquel tablero. Con un análisis retrospectivo termina demostrando “Quién mató al caballero”.

Se parte de que es el turno de las negras. El jugador de la izquierda está más relajado y distraído, mientras que el jugador de la derecha estudia la jugada que le acaban de hacer.

En la posición tenemos un caballo blanco y dos caballos negros, o sea, un caballo blanco fue capturado. La inscripción Quis necavit equitem la podemos traducir como ¿qué pieza se comió al caballo blanco?

En primer lugar hay que deducir cuál fue la pieza negra que realizó el movimiento anterior. Para ello primero se descartan las piezas negras que no han podido mover:

a) No ha podido mover ninguno de los peones negros. Los tres de a7, b7 y d7 se encuentran en sus posiciones iniciales, y el peón de a5, que vino de c7, ya necesitó capturar dos veces antes de que la torre se interpusiera en su camino.

b) No ha podido mover el alfil de c8, puesto que está en su posición inicial. Sus diagonales de salida han estado bloqueadas toda la partida por sus peones de b7 y d7.

c) No ha podido mover el caballo que hay en b8, pues todas las casillas desde donde podría haber venido (a6, c6 y d7) están ocupadas por peones.

d) No ha podido mover el caballo que hay en d1, ya que en las casillas desde donde pudo haber venido (b2 o e3) estaría dando jaque al rey blanco, por lo que ambas jugadas serían imposibles

e) No ha podido mover la torre negra de c1, puesto que sus casillas inmediatas (b1, d1 y c2) están ocupadas.

f) No ha podido mover el rey negro: desde b4 o b3 habría estado en un jaque simultáneo imposible. Desde a3 recibiría otro jaque imposible del caballo blanco, puesto que éste tendría que haber llegado desde c3 o d2 y estas casillas también están ocupadas.

En conclusión, descartadas las demás piezas, el último movimiento de la partida lo hizo la dama negra.

¿Y de dónde vino la dama negra? Tenemos las cuatro hipotéticas casillas: a2, b2, b3 y d3. Descartamos a2, b3 y d3 porque desde estas casillas estaría dando un jaque imposible. Sólo nos queda b2.

Así pues, el último movimiento de la partida lo hizo la dama, que fue de b2 a c2.

Para no extenderme demasiado resumiré el resto. Se deduce que la dama debió retirarse de la columna por la amenaza de las torres blancas, y se investigan diferentes posibilidades. Se demuestra que la torre de g4 no pudo llegar o capturar una pieza negra en b5 y se concluye que una pieza blanca se interponía entre la torre blanca y la dama negra. Finalmente se demuestra que esta pieza sólo pudo ser un caballo blanco (precisamente el que falta en el tablero).

Es decir, el caballo blanco movió de b4 a c2, descubriendo la columna b y dejando la dama negra amenazada por la torre de b4 y fue precisamente allí, en c2, donde la dama negra capturó al caballo.

Y así se obtiene la respuesta a Quis necavit equitem: fue la dama negra la que mató al caballero.

Ello desenmascara al autor de un crimen cometido 500 años atrás, cuyos protagonistas figuran en la propia pintura. Beatriz de Borgoña (la mujer que está leyendo), esposa de Fernando de Ostenburgo (el jugador que conduce las negras), fue la asesina de Roger de Arras (el caballero que juega con blancas).

«Hace tiempo que cambié a Dios por el ajedrez», dijo recientemente Pérez-Reverte en una entrevista. De hecho, el ajedrez está presente varias de sus novelas. En La tabla de Flandes, Pérez-Reverte se inspiró en el libro de Smullyan Juegos de ajedrez y los misteriosos caballos de Arabia, para componer la posición inicial que hemos visto. Después de solucionar el tema retrospectivo la novela sigue la partida hacia adelante y se producen sucesivos hechos reales relacionados con las jugadas que se van sucediendo. Eso ya lo dejo para quien quiera leer y disfrutar el libro. (Ver la partida completa de la tabla de Flandes a partir de la la posición representada en la pintura, comentada por Leontxo García).

Hay problemas retrospectivos donde no es posible determinar la secuencia exacta de los últimos movimientos, pero donde se puede probar qué movimientos se realizaron en algún momento de la partida, como ilustra el último ejemplo (un extracto del libro de Smullyan, The Chess Mysteries of Sherlock Holmes) que os lo dejo para que lo resolvais vosotros.

Dada la siguiente posición la pregunta es: ¿En qué casilla fue capturada la dama blanca?

Vamos a ver. ¿Qué pasó aquí? Ahí van unas pistas. Una de las claves para resolver estos problemas consiste en hacerse las preguntas correctas:
– ¿Qué pieza negra fue capturada por el peón blanco en b3?
- ¿Cuál es la casilla original de esta pieza?
- ¿Qué piezas blancas pudieros ser capturadas en la 6ª fila?
- ¿Qué pieza blanca fue la primera en ser capturada?

Ánimo. Estrujaros la cabeza que de vez en cuando también es sano.

La solución del enigma, narrada por el propio Sherlock Holmes:

En definitiva, si el ajedrez hacia adelante ya es infinitamente profundo, se engrandece aún más con la guinda del ajedrez hacia atrás. En los anteriores ejemplos hemos visto cómo las jugadas de una partida pueden dejar rastros. La disposición de las piezas nos dice que cosas fueron posibles o imposibles. Cuando observamos una posición podemos ver acontecimientos fosilizados. Y el estudio arqueológico de estos fósiles nos desvela el misterio de la vida de la partida que se jugó.