…No es posible encontrar una noción más estética que la reciente
Teoría de las Catástrofes de René Thom, que se aplica tanto a la
geometría del ombligo parabólico como a la deriva de los continentes.
La Teoría de René Thom ha encantado todos mis átomos desde que la
conocí… Dalí, 1985

La teoría topológica de las singularidades y bifurcaciones, conocida como Teoría de Catástrofes (TC), fue introducida por el matemático y filósofo francés René Thom para estudiar los saltos o cambios que se producen en los sistemas dinámicos. Estudia desde el punto de vista matemático lo que vulgarmente se conoce como la “gota que colma el vaso”, esa mínima gota que provoca que el agua se derrame, que se produzca un alud, se derrumbe un edificio, o que un animal pase en un momento determinado al ataque, y se pase de un estado inestable a otro estable.

Intuitivamente, y de forma simplificada (topología “superelemental”), los puntos interiores de un conjunto continuo serían puntos regulares y los puntos que forman su frontera serían puntos catastróficos. Los puntos regulares están rodeados de puntos que tienen la misma apariencia cualitativa en los que no “ocurre nada”, todo sigue igual (continuidad). En los puntos de la frontera o catastróficos siempre“ocurre algo”, pasa de haber una continuidad del sistema a encontrarnos con un cambio radical.__ Esta distinción entre puntos regulares y catastróficos es preliminar no sólo para la teoría de las catástrofes, sino para cualquier disciplina que establezca descripciones sobre cualquier forma teórica__. René Thom demostró que para los sistemas en los que interviene una o dos variables y en los que influyen hasta cuatro parámetros (tiempo, temperatura, gradientes…), hay siete rupturas o catástrofes elementales (morfologías o formas), a las que se han dado nombres muy plásticos e intuitivos: pliegues, cúspides, colas de milano, mariposas y ombligos elíptico, hiperbólico y parabólico.

En palabras suyas:” La TC se esfuerza por describir las discontinuidades que pudieran presentarse en la evolución del sistema.. Intuitivamente, se admite que la evolución global de un sistema se presenta como una sucesión de evoluciones continuas, separadas por saltos bruscos de naturaleza cualitativamente diferente. Para cualquier tipo de evolución continua subsiste el marco del tipo diferencial clásico, pero los saltos hacen que se pase de un sistema diferencial a otro. Se salta de una evolución continua descrita por un sistema de ecuaciones diferenciales a otra evolución continua descrita por otro sistema y no se puede excluir que un número finito de sistemas no sea suficiente para describir la situación por completo.” Realmente, aclara que más que una teoría, es una metodología, o acaso una especie de lenguaje, que permite organizar los datos de la experiencia en las condiciones más diversas.

René Thom ha sabido acercar las Matemáticas a las «morfologías», y ha estudiado con herramientas topológicas la aparición, la estabilidad y la desaparición de formas; ha encontrado el sentido de las cosas, en tanto en cuanto son formas o morfologías, a partir de ciertos invariantes que son las rupturas o singularidades. Así ha podido clasificar las maneras de proceder ante esas rupturas –las famosas «catástrofes» elementales– en sistemas dinámicos, tan variados que pueden ser físicos, linguísticos, biológicos o sociales.

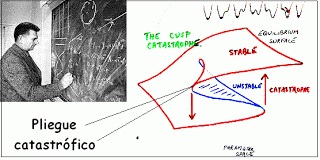
A pesar del fracaso –según los cánones del positivismo– de la TC como teoría científica aplicada, Thom ha abierto las matemáticas a las formas o morfologías del mundo, con el fin de comprenderlo, de encontrar su sentido, y no sólo movidas por el interés de predecir sucesos, clásico ejercicio decimonónico de la ciencia. Y ha empezado a mostrar su poder para hacerlo al permitir acercarse a través de muchos de su conceptos fundamentales –estabilidad estructural, bifurcaciones, atractores…– a la comprensión de fenómenos naturales tan complejos y tan corrientes como «la forma de una nube, la caída de una hoja, la espuma de un vaso de cerveza».

Libro : Parábolas y catástrofes , de René Thom. Una larga entrevista en la que consigue aclarar el sentido profundo de las analogías (“parábolas”) que explican algunos de los más enigmáticos y fascinantes fenómenos discontinuos (o “catástrofes”). René Thom, en los años setenta, desafió en su propio terreno a físicos y biólogos, a economistas y lingüistas, proponiendo, con su teoría de catástrofes, una nueva manera de considerar todas las transformaciones que se producen de modo brusco, imprevisto, dramático.

La primera figura procede de Divulgamat , encontrareis un interesante documento sobre la relación de Dalí con la TC.