
Ciencias y letras, trata de acercar las dos culturas , favorecer su mestizaje. En realidad, sólo es una cultura que nos puede acercar más a nosotros mismos, a las complejas relaciones humanas, al mundo y a sus interrogantes. El autor, ingeniero y físico, es editor de La bella teoría. Publica los días 1 de cada mes.
Realidad y números imaginarios
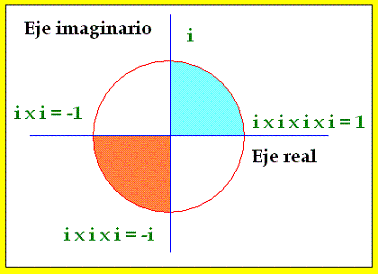
Nada parece más apartado de la realidad que “inventar” un número, llamado“i”, que es la raíz cuadrada de -1. En un mundo imaginario, ese número sería de tal forma que podríamos construir con él un cuadrado de superficie negativa e igual a -1. El producto de cualquier número real por i da como resultado unos números que llamamos imaginarios que, como veremos, no son menos reales que los llamados números “reales” a los que estamos acostumbrados. La suma de un número real y otro imaginario se llama número complejo, por ejemplo el número: 7+ 3i. Estos números suelen representarse en el plano de forma que los reales ocupan el eje horizontal de las x, mientras que los imaginarios ocupan el eje vertical de las y.

El objetivo original de la introducción de los números imaginarios era poder tomar raíces cuadradas sin problemas, pero se han encontrado otras muchas propiedades “mágicas” que poseen estos números en combinación con los reales (números complejos). Estas propiedades aparecen bajo nombres diversos y extraños, como la fórmula integral de Cauchy, el teorema de la aplicación de Riemann o la propiedad de extensión de Lewy, pero su influencia se cuela en infinidad de fenómenos cotidianos, porque está en la propia base de las matemáticas que rigen las leyes de la física.
Nos los podemos encontrar en cualquier sitio, en cualquier expresión matemática pura o relacionada con algo tan prosaico como las relaciones de impedancias en un circuito de corriente alterna. En la función de onda de la mecánica cuántica o en cualquier expresión de naturaleza ondulatoria o periódica. En la técnica, en la física o en las matemáticas más abstractas.
El número i, junto con los números trascendentes PI (relación entre la longitud de la circunferencia y su diámetro) y el e (base de los logaritmos naturales o neperianos), aparece en la más bella expresión matemática que existe, la ecuación de Euler. Esta expresión que liga a tres de los números más importantes de las matemáticas también es un ejemplo de la rica conexión entre los números, sus propiedades y la realidad física de todo orden.
La realidad que vemos y tocamos cada día está ligada de forma inextricable a estos misteriosos números, llamados imaginarios de forma despectiva por René Descartes. Para entenderla en toda su extensión necesitamos de los números reales y de los números imaginarios, de su extraña pero mágica relación.
Comentarios
Textos anteriores
Librería LdN

Comentarios
- Cocina intuitiva (2)
- Baipás (6)
- Los clásicos nunca mueren (1)
- Cerrado por traspaso (2)
- Elogio de la menestra (2)
- La ex ministra, la ex miss y la asimetría en Twitter (3)
- La educación como síntoma (12)
- 29 de diciembre (13)
- Vocaciones de vacaciones (3)
- Marcos Taracido y Alberto Haj-Saleh: “Tenemos guardados todos los contenidos de Libro de Notas en este pen drive de dos gigas” (3)
Suscripción
Publicidad
Publicidad
Esta obra está bajo una licencia de Creative Commons
Desarrollado con TextPattern | Suscripción XML: RSS - Atom | ISSN: 1699-8766
Diseño: Óscar Villán || Programación: Juanjo Navarro
Otros proyectos de LdN: Pequeño LdN || Artes poéticas || Retórica || Librería
Aviso legal
2008-01-01 17:03
Recuerdo en mi libro de mates del colegio el retrato de Cardano en el margen, en aquel misterioso capítulo de los números complejos. Desde entonces hasta hoy esos extraños números me han acompañado. Están presentes en mi trabajo diario, pero no por ello han dejado de fascinarme.
Gracias por el artículo.
2008-01-01 17:37
Gracias a ti por tu precioso comentario.
2008-01-02 19:22
Pues yo recuerdo vagamente todas esas cosas, pero siempre me han fascinado las matemáticas, los números… no puedo darle una explicación, es una atracción extraña, cada vez que veo algo relacionado con el tema lo leo aunque no me entere.
Yo también te doy las gracias.
asalu2
2008-01-04 00:10
La determinada existencia de los números imaginarios, deja claro, que las matemáticas son el campo en el que la creatividad, libertad e imaginación humanas, encuentran su máxima expresión.
No en vano las matemáticas, como la música, son artes-ciencias, de luz.
Precioso artículo, y casi me lo pierdo en la selva mediática.
2008-01-06 22:09
Es una satisfacción ver que he conseguido transmitir un poco de la belleza que tienen las matemáticas. Un saludo.
2008-06-03 00:08
La verdad es que a mi me fascinan las matematicas y me llama poderosamente la atencion los numeros reales porque me encuentro con el animo de construir una teoria matematima que permita hacer real ese aspecto de imaginario, en el entendido de que las matematicas son ciencias exactas y que que se demuestra lo que se afirma. La otra gran verdad es que me encuentro cursando tercer semestre de Ingenieria Química y el tiempo que me queda es muy poco o nada y hay momentos como este semestre que estoy desanimado y olvodo todo; pero quiero enrumbarme frente a esa teroria que la tengo dando vueltas en mi cabeza desde que estaba en décimo grado. muy buena esta toria me va a ser de mucha ayuda, sobre todo frente a otro debate que tengo con fisica cuantik. Chao
2008-06-04 00:00
Bueno Dilson, me alegra la extraordinaria afición que tienes por las matemáticas y te animo a desarrollar las ideas que tengas sobre ellas. Un saludo y cuenta conmigo para lo que necesites.
2008-06-30 21:46
Gracias por el artículo. No estoy muy familiarizada con los números complejos, pero habré de estarlo, ya que para mi trabajo de investigación del instituto he escojido ‘Números complejos y fractales’. Todavía no sé gran cosa, pero todo lo que he visto hasta ahora me engancha a aprender más (y a poder entenderlo).
2008-07-01 13:24
Pues adelante Dana, con lo primero que puedes empezar es con el fractal de Mandelbrot, fractal generado por iteración de números complejos. Un saludo.
2008-09-12 03:03
Es dificil hablar d esactitud por saben q es y cuanto equivalen?: segundo,kilo,centimetro lo inventaron no tiene porq ser esacto.
2008-11-20 15:17
Excelente; primera vez que entro al libro de notas y lo que encuentro es este “Imán”.
Felicitaciones por la coherencia en el desarrollo del contenido.
2008-11-21 14:00
Gracias Octavio. Un saludo.
2009-03-08 20:39
Siempre he tenido curiosidad por lo basico y complejo de las matematicas, hasta en eso se parecen a los numeros complejos, si bien muchas veces vemos la realidad algunas veces es dificil encontrarla; pienso e imagino que la solucion a cualquier problema no solamente esta en una realidad real, si no tambien en una realidad mas exacta la cual pudiera llamarse “realidad imaginaria”
2009-03-09 13:49
Sea como sea, tal como comento en el último párrafo,la realidad que vemos y tocamos cada día está ligada de forma inextricable a estos misteriosos números. Para entenderla en toda su extensión necesitamos de los números reales y de los números imaginarios, de su extraña pero mágica relación.
Un saludo Jose.
2009-03-28 00:53
me parecen numeros fascinantes, son tan complejos mas a simple vista parecen tan sencillos es una maravilla son tan magicos y maravillosos y fascinantes, a pesar q los veia extraños cuando estava en 6º grado hoy en dia siento una gran intriga y a la vez una gran fascinación!
gracias x el artículo.
2009-03-29 22:37
Gracias a ti Michelle. En el próximo artículo hablo de ángulos y triángulos, de las relaciones trigonométricas, de cómo surgieron desde un interés, eminentemente práctico. Al final también vienen a desembocar en estos “mágicos” números.
Saludos.
2010-05-13 20:23
gracias por despertar la curiosidad.
Sabes de algun articulo o fuente que expique ampliamente como se dio el echo de aplicar algo tan abstracto cómo lógico a la física cuántica de andar por casa?
2013-07-18 04:20
No debe faltar aquí la génesis de los números imaginarios, el teorema fundamental del álgebra, gauss demostró que el resultado general de un polinomio de grado n tiene n raíces complejas siendo las reales aquellas con la parte imaginaria igual a cero, ejemplo en x^3=8 x no vale solamente 2 no sean ingenuos, pero mas importante aun esta el hecho de que esto revela que el plano complejo esta intrínsecamente relacionado con la operatividad de cuadrar, un plano complejo la magnitud y fase “cuadra” algo, por lo que un área negativa no es algo imposible es algo que es posible si lo ves del punto de vista de cuadrar, abre los ojos, para los que sinceramente quieran saber como es esto lean a gauss, el principe de las matematicas, el sabe.
2013-07-19 15:49
Gracias por tu aportación Héctor. Creo que la génesis ha quedado clara hasta donde yo quería llegar. En una próxima ocasión me parece muy bien hablar del gran matemático Gauss y de su obra. Un saludo.