Resulta sorprendente como la resolución de problemas aparentemente intrascendentes, como colocar 6 monedas iguales tangentes a otra del mismo tamaño, puede llevar a solucionar cuestiones tan importantes como la propia estructura del universo. La clave última de esta conexión está en la simetría: en términos matemáticos, debajo de todo objeto simétrico yace una estructura matemática llamada grupo . Ejemplos típicos de objetos tridimensionales simétricos son la esfera, el cilindro o el cono.

Todos sabemos como colocar 6 monedas iguales tangentes a otra moneda del mismo tamaño. En una dimensión superior podemos colocar doce esferas, cuidadosamente apiladas, de forma que cada una de las cuales toca a una esfera central. Pero no se conoce cual es el número óptimo en ninguna dimensión superior a 3, excepto en dimensión 8, donde el grupo E8 nos proporciona un retículo en el que cada esfera toca a otras 240 (y en dimensión 24, que el retículo de Leech nos permite colocar 196560 esferas de dimensión 24 tangentes a una esfera central). El objeto matemático que permite esta proeza en 8 dimensiones se cree, desde hace tiempo, que puede jugar un papel importante en la teoría capaz de unificar todas las interacciones y partículas elementales existentes.

Un poquito sobre teoría de grupos:

El grupo es una estructura matemática, en principio muy sencilla, que se establece a partir de un conjunto G con una operación “ º “ tal que aplicada a sus miembros da como resultado otro miembro del conjunto (operación interna). Esta operación tiene las siguientes propiedades:

Asociativa: Para todo g1,g2,g3 pertenecientes a G se cumple que (g1 º g2) º g3 = g1 º (g2 º g3).
Elemento neutro: Existe un elemento neutro e, perteneciente a G, tal que para cualquier elemento g del conjunto G : e º g = g º e = g . Como ocurre con la unidad para el producto, o el cero para la suma de números enteros.
Elemento inverso o simétrico: Para todo g perteneciente a G, existe un elemento llamado inverso_de_g tal que: g º (inverso_de_g) = (inverso_de_g) º g = e ( donde e es el elemento neutro).

Si además se cumple que g1 º g2 = g2 º g1 , o propiedad conmutativa, entonces el grupo se llama abeliano.Esto que en el instituto nos creíamos que sólo valía para enredar y darnos la lata, nos puede ayudar a desentrañar los misterios de la composición íntima de nuestro universo.

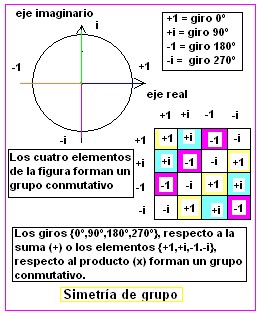
Como ejemplo, podemos ver en la figura un grupo compuesto por cuatro elementos, las potencias del número imaginario i que es la ráiz cuadrada de -1, o las rotaciones de 0º, 90º,180º ó 270º. Bien con la suma o con el producto, como operaciones de composición interna, vemos que podemos establecer un cuadro en donde observamos todas las relaciones entre los elementos del grupo. La propiedad conmutativa le confiere una simetría completa al cuadro.

En este grupo sólo necesitamos una tabla de 4 × 4, imáginemos la complejidad y la simetría tan maravillosa que encierra el grupo E8 que necesita de una tabla 453060 × 453060 para expresar las relaciones entre sus elementos.

Como nos ayuda la estructura de grupo:

Apoyándonos en el grupo sencillo de la figura podemos hacernos una idea de como nos ayudan los grupos en nuestra búsqueda del conocimiento de las partículas elementales y sus interacciones. Supongamos que este grupo nos muestra una simetría que refleja la relación de tres partículas conocidas mediante cierta interacción. Cuando analizamos el problema nos damos cuenta de que para completar la relación entre ellas necesitamos de otra partícula desconocida para completar el cuadro. En base a simetrías matemáticas podemos saber como será esa partícula y como se relaciona con las demás, además ese conocimiento nos permitirá diseñar experimentos para detectarla.

De hecho, experimentos tan grandiosos como el del LHC ( Gran Colisionador de Hadrones), que ha atraído nuestra atención estas últimas semanas, no habrían sido posibles sin la ayuda de las matemáticas subyacentes de la discreta teoría de grupos.